Escaping the Odds and a Formula for Life

Abstract

We all make bets in life—on our careers, relationships, and decisions. This is a personal story that might change how you approach your own bets, too.

From an escape room adventure in Vegas to an obsession with the perfect betting strategy, a friend’s simple question—How should I bet to maximize my returns?—led me down a rabbit hole of math and puzzles, ultimately uncovering the Kelly Criterion. As I deciphered the formula, I realized it extends far beyond finance or gambling. This is a story of escape, in more ways than one.

What Happened in Vegas Didn’t Stay in Vegas

A few times a year, my two closest friends and I meet in a new city to reconnect and recharge. We all live in different parts of the U.S., so it’s our chance to catch up. Our latest hobby? Escape rooms—and no, we’re not exaggerating when we say we do three or four of them back-to-back.

This time, we chose Las Vegas.

Our partners think our hobby is strange, but not as much as the taxi drivers who drop us off at sketchy spots on the outskirts of Vegas.

"Oh, it’s an escape room," we say casually. "We lock ourselves up in a room and solve puzzles to escape." Best leave the rest to their imagination.

Over coffee before our session, my friend Chris shares his latest side project: an AI/ML model to predict (American) football games. As a software engineer and sports fanatic, he’s eager to test his model with a few bets.

He poses a question: "Given a set of predictions, how should I bet to maximize my return?"

We pause. "What do you mean?"

"My model predicts the probabilities of teams winning. Based on that, I want to figure out the best way to place my bets."

"Don’t payouts affect your decision? A higher payout would influence your bet, right?"

"Exactly. I want to factor in the expected returns and bet on games with favorable odds," he says.

"And what about confidence intervals? Shouldn’t your model’s confidence in each prediction guide your bet?"

He nods but waves it off. "I want to keep it simple. I just want to know how to spread my bets. I can’t drop all my money on one game. If I lose, it’s over. I need to diversify."

We pause, thinking.

"It really comes down to two questions," Chris says.

How much should I bet on each game?
How many games should I bet on to diversify?

We glance at the time. "We’re almost late. Let’s go!" We quickly grab our stuff and head out.

Caught in the Vegas Trap

I don't remember how we fared in that escape room. Knowing our competitive group, we probably crushed it.

But the betting puzzle? It followed me back home—gnawing at the back of my mind for days, weeks, then months. The question had become its own Vegas-themed trap. To escape, I needed to find the optimal strategy.

Then one day, I stumbled upon DJ's YouTube video on the Kelly Criterion—a strategy for optimal betting.

Eureka! The formula? Simple:

f^* = \frac{bp - q}{b}

Where:

$f^*$ is the fraction of your bankroll to bet
$b$ is the multiple of your bet that you can win (i.e., the odds)
$p$ is the probability of winning
$q$ is the probability of losing (i.e., $1 - p$ )

Suddenly, a clue to Chris’s puzzle was right there in front of me.

Take a biased coin that lands heads $55\%$ of the time. The payout is $1:1$ . Plugging it into the Kelly Criterion gives you:

f^* = \frac{bp - q}{b} = \frac{(1)(0.55)-0.45}{1}=0.10

That means you should bet $10\%$ of your bankroll.

What in the world...? How? Why? Who? When?

I had two choices: accept the formula and move on with my life or take the red pill and enter its maze.

There was only one real choice. Knowing the Kelly Criterion wasn’t enough. To escape its grips, I had to understand it.

And so, I took the plunge.

How did a once quiet academic paper become the go-to tool for gamblers, investors, and hedge fund managers alike? Fortunately, DJ's video hinted at a few resources that became my guide. What followed were months of confusion, discovery, and awe as I read the following papers and books ¹:

Paper: A New Interpretation of Information Rate by John L. Kelly Jr.
Paper: A Mathematical Theory of Communication by Claude E. Shannon
Book: Fortune's Formula by William Poundstone
Book: A Man for All Markets by Edward O. Thorp
Book: The Man Who Solved the Market by Gregory Zuckerman

Chasing the Intellectual Gamble

The Kelly Criterion isn’t just about betting or finance—it’s about the power of compound growth.

"Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it."

~Albert Einstein (maybe)

To grasp its full potential, I explored its history filled with some of the greatest minds in math and finance.

In 1956, John L. Kelly Jr., a Bell Labs researcher, inspired by Claude Shannon’s work in information theory, applied Shannon’s insights to a new problem: optimizing bet sizes to maximize long-term capital growth. The result? A formula that would become a cornerstone for gamblers, investors, and hedge funds alike.

But, what is the Kelly Criterion really about?

Given the geometric growth as $G=\frac{W_n}{W_0}$ , where $W_0$ is the initial capital and $W_n$ as the final capital after $n$ trades, the Kelly Criterion maximizes $\mathbb{E}[log(G)]$ . In other words, the Kelly Criterion maximizes the expected logarithm of the geometric growth.

That was the key. But understanding it? Not so easy.

I repeated the phrase over and over, emphasizing different words, trying to make sense of it: "maximizes… the expected… logarithm… of geometric growth." Nothing clicked. Yet it became my roadmap:

What is geometric growth $G$ ?
Why maximize the expected $log$ of $G$ ?
How is the Kelly Criterion derived from maximizing $\mathbb{E}[\log(G)]$ ?

With excitement and doubt: Will I be able to understand it at the level I want? Is this even useful for Chris’s betting problem?

There's only one way to find out.

Worst case, I’ll explore fascinating topics from some of the most brilliant minds, I told myself, justifying the journey ahead.

A quick pit stop before we dive headfirst into the math. The next section, Cracking the Code, is where things get a little dense—it’s math territory. Don’t panic! I’ve broken it down step by step, so even if math gives you chills, you’ll see that it's simple and beautiful. Think of it like deciphering a treasure map: the path might twist and turn, but the gold at the end is worth it. But hey, if math isn’t your cup of coffee, no worries! Skip ahead to the section Betting for Survival, and we’ll get back to the fun stuff. Your call, your adventure.

Cracking the Code

Looking to understand the formula, I kept coming back to its essence. The Kelly Criterion is about balance: not risking too much to avoid ruin, while not risking too little to ensure long-term growth.

With that thought, the journey began.

(1) What is geometric growth $G$ ?

The first step was understanding geometric growth. To do that, I needed to revisit the difference between the arithmetic and geometric mean.

Arithmetic mean vs geometric mean

The arithmetic mean is straightforward—it’s the average of a set of numbers:

\text{Arithmetic Mean} = \frac{x_1 + x_2 + \dots + x_n}{n}

For example—and to cater to a broader audience beyond (American) football—let's look at Lionel Messi's goals over $5$ games: $3,2,1,3,1$ . The arithmetic mean (average) is:

\text{Average \# goals} = \frac{3 + 2 + 1 + 3 + 1}{5} = \frac{10}{5} = 2

An average of two goals per game. Not bad. Almost as good as my average playing FIFA 99—ah, the golden days.

The geometric mean, though, is what matters for compound growth. It measures outcomes that build on each other:

\text{Geometric Mean} = (x_1 \times x_2 \times \dots \times x_n)^{\frac{1}{n}}

Since goals don’t compound (though Messi’s fanbase seems to), a better example is financial returns. Say you earn returns of $1.1$ , $1.2$ , and $0.9$ (representing $10\%$ gain, $20\%$ gain, and $10\%$ loss). The geometric mean is:

\text{Geometric Mean} = (1.1 \times 1.2 \times 0.9)^{\frac{1}{3}} \approx 1.0591

This represents an average growth rate of $5.91\%$ . If you started with $\$100$ , you’d end up with about $\$118.80$ after three periods, validated by:

(100)(1.0591^3) \approx \$118.80

However, if we use the arithmetic mean to estimate the growth rate:

\text{Arithmetic Mean} = \frac{1.1 + 1.2 + 0.9}{3} \approx 1.066

This suggests an average growth of $6.6\%$ , which gives $\$121.14$ . Clearly, that’s wrong. The geometric mean is what accurately captures the true compounded growth.

That's interesting, though. Is the arithmetic mean always larger than the geometric mean? Yup, it is always the case:

\text{Arithmetic Mean} \geq \text{Geometric Mean}

So why does the Kelly Criterion maximize the geometric growth? That’s where the magic of compounding comes in.

Arithmetic growth vs geometric growth

The arithmetic mean looks at a simple average of returns, without considering the effects of compounding. For example, if you gain $50\%$ and then lose $50\%$ , the arithmetic growth says you break even:

\frac{1.5 + .5}{2} = 1

But the geometric mean paints a more accurate picture:

(1.5 \times 0.5)^{\frac{1}{2}} \approx 0.866

So, your overall return isn’t zero—it’s negative! The geometric mean captures the real average growth rate over time. Negative in this case. While the arithmetic mean suggests you’re breaking even or better, the geometric mean is what matters when it comes to long-term growth.

Bingo! The Kelly Criterion maximizes the geometric growth because it's a more accurate view of multiplicative returns. While the arithmetic mean may be larger, the geometric mean grows faster as returns compound.

(2) Why maximize the expected $log$ of $G$ ?

To $\log$ or not to $\log$ ? That seems to be what cool kids ask these days.

The Kelly Criterion tells us to $\log$ . But, why?

Behold, the logarithm

Let's start with a quick reminder that logarithms answer: "To what power must a base (usually $10$ or $e$ ) be raised to produce a given number?" ² For example, the logarithm of $100$ to the base $10$ is $2$ , because $10^2 = 100$ .

If thou art like me, and dost favor $0$ s and $1$ s, to what great powers shall mere mortals raise their $2$ and be granted $8$ ? Verily, thou shalt receive $3$ .

log_2(8) = 3

I like to think of the logarithm as the yin to the yang of exponential growth: it simplifies describing geometric growth and the process of compounding.

"How does it do that?" you may ask.

Let me let you in on a (well-known-but-often-forgotten-after-middle-school) secret that logarithms simplify multiplication into addition:

\log(a \times b) = \log(a) + \log(b)

When we deal with periods of compounded growth (which involves multiplying returns over time), the math can get complicated. Logarithms are a powerful tool to simplify this calculation.

For example, if your wealth grows by $10\%$ , $5\%$ , and $15\%$ over three years, you calculate the final wealth as:

W = W_0 \times (1.1)(1.05)(1.15)

Logarithms simplify this process:

\log(W) = \log(W_0) + \log(1.10) + \log(1.05) + \log(1.15)

It’s much easier to add logs than multiply several terms. Once added, you can exponentiate to return to actual wealth:

W = \exp(\log(W))

Now let's get to the key point: why does the Kelly Criterion use $\log$ ? It's not just be about making the calculations easier, right?

Greed is good—up to a certain point

We all have expectations—some loftier than others. To achieve true happiness, it’s critical to reflect on those expectations and set proper boundaries.

"Wait a second, are we discussing the Kelly Criterion or diving into relationship advice?"

"Ah, excellent question!" I reply with a sly smile. "Funny enough, managing expectations and setting boundaries is the secret sauce to maximizing long-term success in both finance and life."

"Touché. Well played."

Logarithms capture the risk/reward trade-off, penalizing large losses more than they reward large gains. The concave shape of the log function means that as wealth increases, the utility of each additional gain diminishes. The logarithmic utility reflects the reality that aggressive bets may lead to big wins, but they also heighten the risk of losing everything.

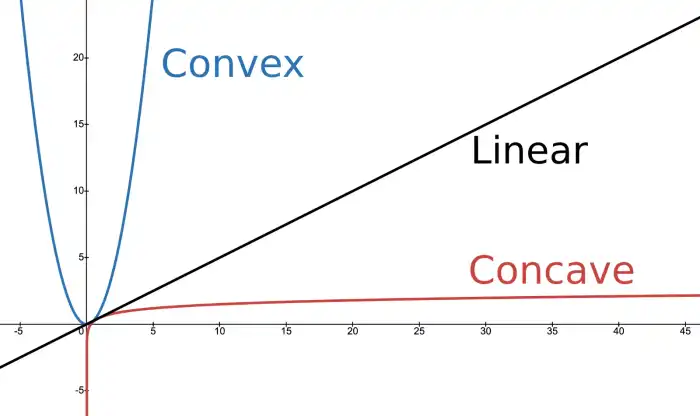
Next time someone says "greed is good" hit them with: "Well, that depends on your perspective." Then casually add, "If you’re truly committed to greed, you’d better play the long game and elawg."

Yes, you heard right. Elawg: the new slang for $\mathbb{E}[\log(G)]$ . You’re welcome.

What happens to who don't $\mathbb{E}[log(G)]$ ?

If we didn’t use the logarithmic utility and focused purely on maximizing expected return, we may take on risky bets that could wipe us out. By using the logarithmic utility, we balance greed with caution—sustainable growth over time becomes the goal.

Let's look at a few concrete examples to illustrate the point.

Scenario 1: No logarithmic utility

Let’s assume you have an initial wealth $W_0 = \$100$ and two possible outcomes from a bet:

$50\%$ chance to double your wealth
$50\%$ chance to lose half of your wealth

Without using logarithms, your possible wealth after the bet are:

If you win: $\$100 \times 2 = \$200$
If you lose: $\$100 \times 0.5 = \$50$

The expected wealth after one round of betting is:

\mathbb{E}[W] = (0.5)(200) + (0.5)(50) = 100 + 25 = 125

The arithmetic expected return suggests that, on average, you’ll end up with $\$125$ . If you follow this strategy and keep betting large amounts, a bad streak of losses will eventually wipe you out. Maximizing arithmetic growth is dangerous; it doesn’t consider the volatility or the risk of large losses.

Scenario 2: Using logarithmic utility (penalizing large losses)

Let’s apply logarithmic utility to the same scenario. Instead of calculating the expected wealth directly, we’ll calculate the expected logarithm of wealth, which better reflects the real risk.

Let’s calculate the logarithms of the outcomes:

If you win: $\log(200) \approx 5.298$
If you lose: $\log(50) \approx 3.912$

Then, calculate the expected logarithmic utility:

\mathbb{E}[\log(W)] = (0.5)\log(200) + (0.5)\log(50) \approx 4.605

The expected log-utility value is $\approx 4.605$ .

To interpret this value in terms of wealth, we exponentiate it:

\exp(4.605) \approx 100

This shows that your expected wealth is $\approx \$100$ . This is much lower than the arithmetic expected return of $\$125$ .

It's starting to make sense. The logarithmic utility function provide a more realistic picture of the risk associated with the bet. While the arithmetic mean suggested an average outcome of $\$125$ , the logarithmic approach shows that you are not likely to increase your wealth on average. It shows that you’re just as likely to end up with something closer to your starting value of $\$100$ .

The logarithmic utility function penalizes the loss of wealth more heavily than it rewards the equivalent gain. The $50\%$ loss is felt more strongly in terms of utility than the $100\%$ gain, and the logarithmic function reflects this asymmetry:

If you lose $50\%$ of your wealth, you’ll have half as much to bet with next time
If you to recover from that loss, you need a 100% gain just to get back to where you started

Let’s take a more extreme scenario to drive the point home.

Suppose instead of betting a reasonable fraction of your wealth, you bet $100\%$ of it on a single round:

If you win: You double your wealth to $\$200$
If you lose: You lose everything, down to $\$0$

Using the logarithmic utility:

If you win: $\log(200) \approx 5.298$
If you lose: $\log(0) = -\infty$ (this is $\text{undefined}$ in practical terms, but it means ruin—you’ve lost everything)

The logarithmic function heavily penalizes the loss of everything because $\log(0)$ results in "negative infinity." This emphasizes that you cannot recover from complete ruin, no matter how large the gains might be in other outcomes.

Given those two options where one protects you from $-\infty$ ruin, the choice is clear: it's better to $\mathbb{E}[\log(G)]$ .

To convince your friends, you can construct a psuedo-Pascal-like argument for tradeoffs between finite and infinite returns. Then, you should reconsider your friends if they are persuaded by Pascal's wager.

We can now use the puzzle pieces to derive the Kelly Criterion itself.

(3) How is the Kelly Criterion derived from maximizing $\mathbb{E}[log(G)]$ ?

By telling you what fraction of your wealth to bet, the Kelly Criterion seeks to maximize the long-term growth of wealth. Let's see how it gets to that conclusion.

Let's define the variables:

$f$ : The fraction of your current wealth to bet
$p$ : The probability of winning the bet
$1-p$ : The probability of losing the bet
$b$ : The odds or return multiplier if you win
$W_0$ : Your initial wealth (bankroll) before placing a bet
$W$ : Your wealth after placing the bet (this is what we want to maximize)

If you win, your wealth increases based on the fraction of your wealth that you bet and the bet odds $b$ :

W = W_0 + fbW_0 = W_0(1 + fb)

And, if you lose, you lose the fraction $f$ of your wealth that you bet:

W = W_0 - fW_0 = W_0(1 - fb)

These two equations together define what happens to your wealth after a bet, either winning or losing.

The next step is to calculate the expected wealth after one bet. Expected wealth is the average wealth you can expect based on the probability of winning or losing:

\mathbb{E}[W] = p\times W_0(1 + fb) + (1 - p) \times W_0(1 - fb)

This gives us the expected wealth after one bet.

As noted earlier, to maximize long-term growth, we want to use logarithmic utility. The logarithm of wealth reflects how returns compound over time. It also penalizes large losses more than it rewards large gains (which matches real-world risk aversion).

Let's introduce $\log$ and factor out $W_0$ , since it’s a constant and doesn’t affect our calculations for finding the optimal ratio::

\mathbb{E}[\log(W)] = p \times \log(1 + fb) + (1 - p) \times \log(1 - fb)

This is the key equation: it represents the expected logarithmic growth of wealth, and our goal is to find the value of $f$ (the fraction of the bankroll to bet) that maximizes this expression.

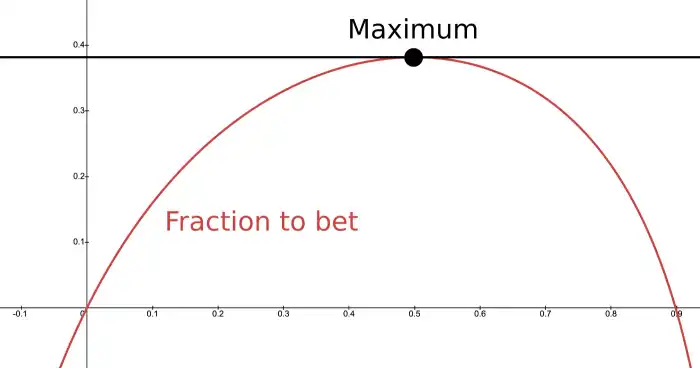
To find the optimal value of $f$ , we call up our trusty pal, Calculus. He sighs, "Oh, so you only call when you need something?" We reply, "I swear, it’s just one tiny calculation—and next time, I'll use limits to make it easy."

To find the maximum, we differentiate the expected logarithmic utility with respect to $f$ and set the derivative equal to zero:

\frac{d}{df}(p\log(1 + fb) + (1 - p)\log(1 - fb)) = 0

The full derivative becomes:

\frac{bp}{1 + fb} - \frac{1 - p}{1 - fb} = 0

Now, we solve for $f$ with some algebra:

f^* = \frac{bp - (1 - p)}{b}

Wait, a minute! That looks super familiar. That is the Kelly Criterion formula:

f^* = \frac{bp-q}{b}

Where:

$f^*$ is the fraction of your bankroll to bet
$bp$ is the expected gain from a winning bet
$q$ is the probability of losing (i.e., $1 - p$ )

Simple. Yet so powerful.

If you're curious how this relates to information theory, they both involve maximizing growth under uncertainty ³.

Now that we've cracked the code, it's time to test it.

Betting for Survival

The sound of grinding metal fills the room as we awaken. We’re seated at a small, cold table, a single coin resting in the center. The dim light casts long shadows, and across the room, a timer begins to count down: 60 minutes.

Suddenly, a familiar mechanical voice fills the room.

"You’ve spent your lives chasing big wins, gambling recklessly, relying on luck and blind faith. Your poor choices have led you here. Now, let’s see if you can make the ultimate gamble for survival."

A screen flickers to life, displaying a simple coin flip. But this time, the stakes are deadly. We have $\$10$ and just one hour to escape. To escape, we have to $10x$ our money.

"I offer you one final chance. Each coin flip can either double your bet or reduce it to ruin. Bet too much, and a single bad flip will destroy you. Bet too little, and you’ll never leave this room."

"To survive, you must turn your $\$10$ into $\$100$ before time runs out."

The voice cuts out. The timer ticks down—59 minutes remaining.

We exchange nervous glances. The first few flips are cautious, every motion deliberate as we calculate the stakes.

Flip. Heads. Small win. Flip again. Tails. Take a hit.

Then, something feels wrong.

"Hold on…" you mutter, grabbing the coin and inspecting it closely. The weight, the shape—something is off.

You scan the room, searching for clues. On the far wall, half-hidden in shadow, you spot a cryptic inscription etched into the metal:

"All men die, but not all men truly live. Sometimes, a 51% chance is all you need to raise your head and find glory."

You pause, frowning. "51%... head..."

It suddenly hits you. The coin is biased: $51\%$ heads, $49\%$ tails.

Heart pounding, you quickly scribble out the formula:

f^* = \frac{(0.51)(1) - 0.49}{1} = 0.02

"We need to bet $2\%$ of our wealth on heads each time. It’s our only shot."

The tables turned. Flip. Heads. Up. Flip again. Tails. Down. Every flip is a blur, the timer a constant reminder of the stakes.

50 minutes left.

We’re sweating, calculating, chasing the perfect bet. Flip. Heads. Up. Flip again. Tails. Down again.

10 minutes left. The room feels like it’s closing in, every flip a heartbeat.

1 minute remaining.

With shaking hands, you toss the coin one last time. Heads.

Our total hits $100 just as the clock runs out.

We’re free.

The door creaks open, and the voice returns, cold and detached: "You’ve escaped… for now."

We stumble out, drenched in sweat, clutching the coin. We survived—barely—but we’ll never look at a coin flip the same way again.

From Survival to Growth

As the door creaks open and I step out of the room, I am blinded by the light.

As my eyes adjust, a profound realization washes over me: I’ve escaped not just the room, but the narrow way I’ve viewed growth.

Like Plato’s Allegory of the Cave. I’ve spent my life chasing shadows, fixated on immediate wins, recklessly betting on short-term outcomes. But now, outside the room, I see the truth—Plato's forms and the ideal bet.

True growth isn’t about maximizing every short-term gain; real growth is geometric, compounding, and it extends far beyond finance or gambling.

I now see the questions my friend asked in a different light:

How much should I bet on any given game?
How many different games should I consider to diversify my bets?

These questions are one and the same. If we're confident in our Kelly Criterion calculations ⁴, we should maximize $\mathbb{E}[\log(W)]$ to balance risk and reward.

Reflecting on the Kelly Criterion, I realize it’s more than just a formula—it’s a philosophy. It naturally complements ideas like Antifragility, which explains why Nassim Taleb wrote the foreword to Edward Thorp’s memoir A Man for All Markets.

The Ultimate Bet

Just as the area of a square grows geometrically, so can our wealth, skills, mindsets, and relationships. These are the true foundations of success. The Kelly Criterion reminds us to avoid instant gratification and instead prioritize long-term, compounding growth.

Now, the choice is yours: What will you bet on? And how will you ensure that your decisions maximize growth—not just for today, but for the future?

As for us, we’ll keep investing in the greatest asset—our friendship—compounding it over time, proving that the richest returns come not from numbers, but from the bonds we build.

Tall Yev, buff Chris, and handsome Farhad @ escape rooms

Of the referenced materials, I highly recommend reading: John L. Kelly Jr.‘s A New Interpretation of Information Rate, which introduces the Kelly Criterion, and William Poundstone’s Fortune's Formula, which offers an engaging exploration of how Kelly’s work influenced gamblers and investors.
↩
In fields like economics, finance, and information theory, the term $\log$ often refers to the natural logarithm $\ln$ .
↩
Shannon’s formula for the capacity of a communication channel is:
↩

C = B \log_2\left(1 + \frac{S}{N}\right)

Where:

$C$ is the channel capacity
$B$ is the bandwidth
$\frac{S}{N}$ is the signal-to-noise ratio

This formula shows the maximum rate at which information can be reliably transmitted over a noisy channel, similar to how the Kelly Criterion shows the maximum rate at which wealth can grow under uncertainty.

Key considerations for applying the Kelly Criterion:
↩

Kelly variants: Betting full Kelly can be psychologically draining, especially with volatile outcomes. Many find that betting half or quarter Kelly reduces emotional swings while still capturing significant long-term growth.
Estimating probabilities: The Kelly Criterion hinges on knowing the true probabilities. But estimating these is often a challenge. Leveraging statistical methods (e.g. Bayesian) can refine our estimates with confidence intervals.
Dynamic environment: The Kelly Criterion assumes static conditions, but in the real world, things change. Betting limits, fluctuating odds, and new information can shift the landscape. Flexibility is key—adapting your strategy as necessary is vital.

Escaping the Odds and a Formula for Life

Abstract

What Happened in Vegas Didn’t Stay in Vegas

Caught in the Vegas Trap

Chasing the Intellectual Gamble

Cracking the Code

(1) What is geometric growth $G$ ?

Arithmetic mean vs geometric mean

Arithmetic growth vs geometric growth

(2) Why maximize the expected $log$ of $G$ ?

Behold, the logarithm

Greed is good—up to a certain point

What happens to who don't $\mathbb{E}[log(G)]$ ?

Scenario 1: No logarithmic utility

Scenario 2: Using logarithmic utility (penalizing large losses)

(3) How is the Kelly Criterion derived from maximizing $\mathbb{E}[log(G)]$ ?

Betting for Survival

From Survival to Growth

The Ultimate Bet

How My Genius Roommate Changed My Perspective

Connect

Abstract

What Happened in Vegas Didn’t Stay in Vegas

Caught in the Vegas Trap

Chasing the Intellectual Gamble

Cracking the Code

(1) What is geometric growth GGG?

Arithmetic mean vs geometric mean

Arithmetic growth vs geometric growth

(2) Why maximize the expected logloglog of GGG?

Behold, the logarithm

Greed is good—up to a certain point

What happens to who don't E[log(G)]\mathbb{E}[log(G)]E[log(G)]?

Scenario 1: No logarithmic utility

Scenario 2: Using logarithmic utility (penalizing large losses)

(3) How is the Kelly Criterion derived from maximizing E[log(G)]\mathbb{E}[log(G)]E[log(G)]?

Betting for Survival

From Survival to Growth

The Ultimate Bet

How My Genius Roommate Changed My Perspective

(1) What is geometric growth $G$ ?

(2) Why maximize the expected $log$ of $G$ ?

What happens to who don't $\mathbb{E}[log(G)]$ ?

(3) How is the Kelly Criterion derived from maximizing $\mathbb{E}[log(G)]$ ?